(비전공자 CS 공부) 컴퓨터과학과 실습 2편 - Digital Logic gate

1편 웜업으로 시작합니다.
이하 배울 내용은 Combinational Logic Circuit과 Sequential Logic Circuit인데 주요한 차이점은 output이 현재 input에 100% 의존적이냐 아니냐이다. 즉, 현재 input이 정해지면 출력값이 100% 정해지는 것은 조합 논리 회로, 현재 input이 있지만 또 다른 input에 따라 결과가 바뀔 수도 있는 것이 순차 논리 회로라고 보면 된다.
순차 논리 회로는 내부에 상태(과거 input)를 저장하고 있다는 것이 주요 특징인데, 주요 조합 논리 회로를 살펴본 후 순차 논리 회로를 살펴보도록 하자.
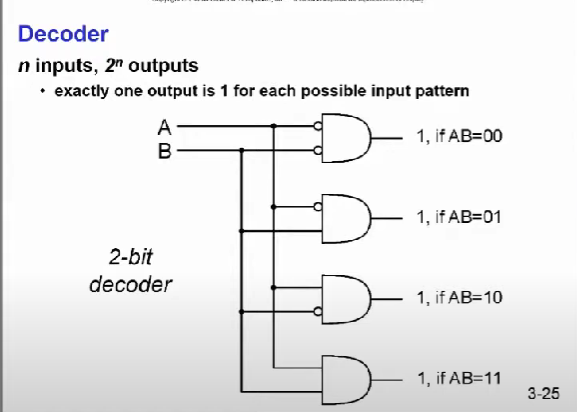
먼저 살펴볼 조합 논리 회로는 Decoder입니다.
특징은 input이 n개면 출력이 2^n개 이며 각 인풋의 조합(Combinatin)마다 2^n개의 출력값중에서 출력값이 1이 되는 것은 단 1개 밖에 없다.
위 이미지의 Decoder 그림 옆에 AB가 00부터 11일 때 각 게이트에 인풋을 대입해 연산해보면 출력이 1이 되는 게이트는 하나 밖에 없음을 알 수 있습니다.
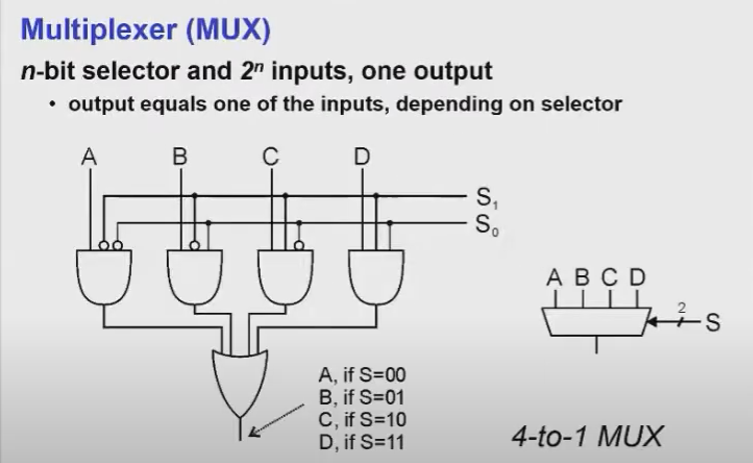
멀티플렉서는 Selector라는 인풋에 따라 각 게이트에 입력되는 인풋(A ~ D)값 자신이 출력되는 기능을 가지고 있다.
위 회로에 Selector와 각 인풋들을 대입해 진리표를 그려보면 다음과 같다.
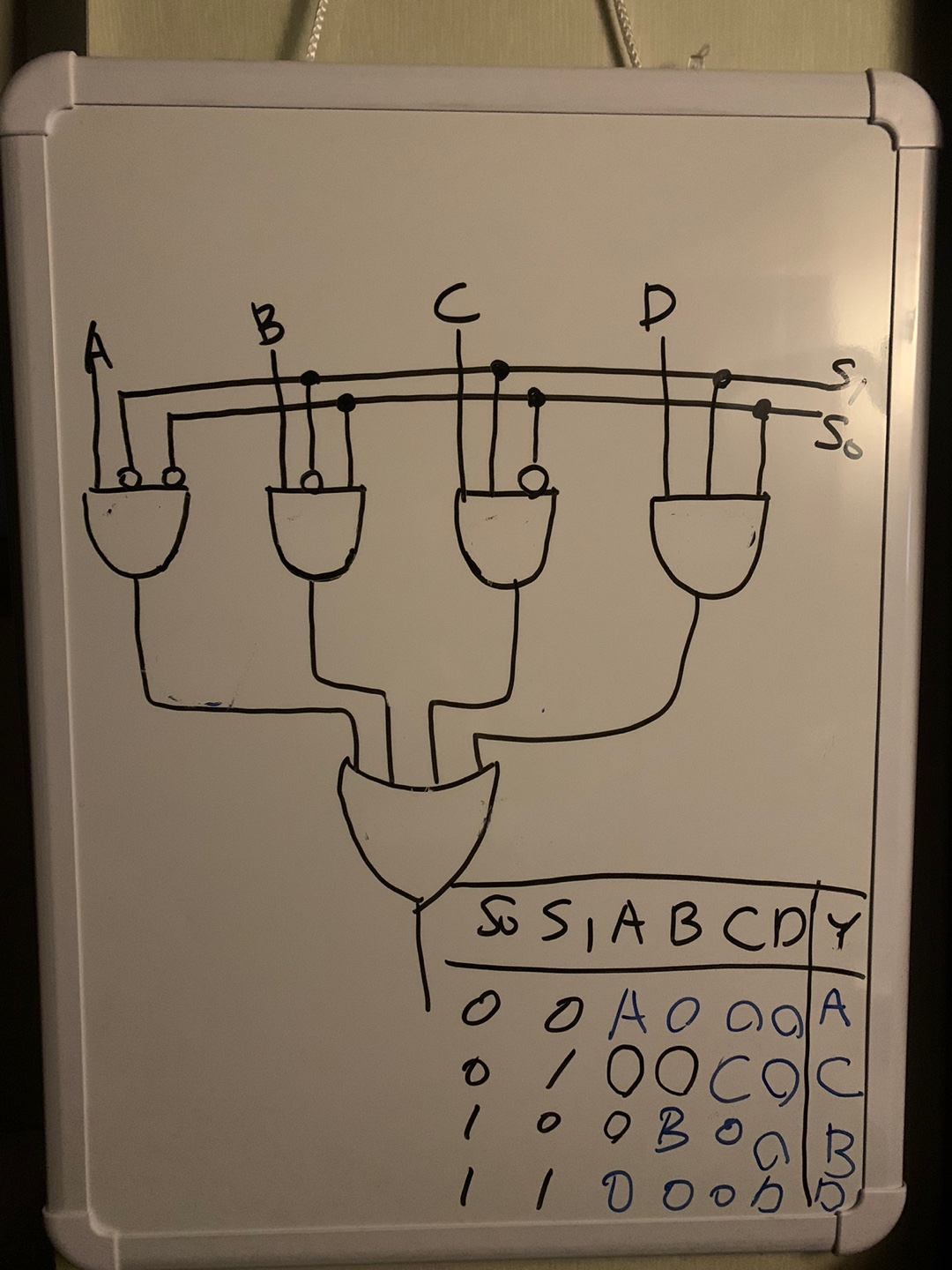
이렇게 진리표를 통해 각 인풋값들을 연산해보면 인풋값 자기 자신이 출력값이 됨을 알 수 있다.
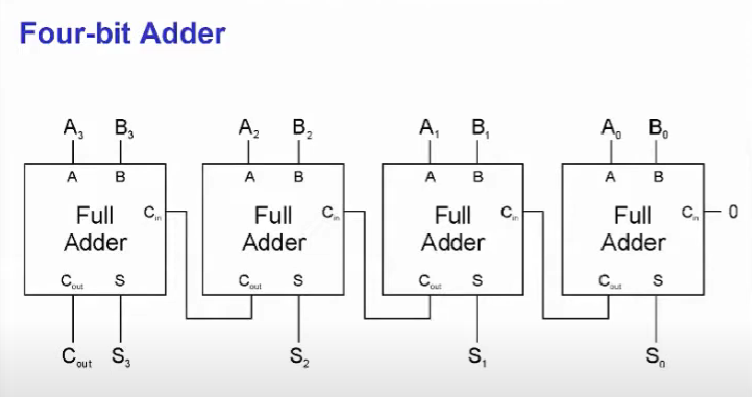
그리고 비트 간 덧셈을 논리 게이트를 통해 만들 수 있는데 임의의 비트 A0과 B0을 대입한다고 했을 때 가장 작은 비트에는 올림수가 올라올 수 없으므로 Carry in을 0으로 가정하고 S에는 해당 자리에 올 값을 그리고 Carry out은 올림수로 다음 자리에 Carry in으로 들어가게 되어 4비트 Adder를 구현할 수 있습니다.
위 4비트 Adder의 구성요소는 Full Adder라는 회로인데 다음과 같이 생겼다.
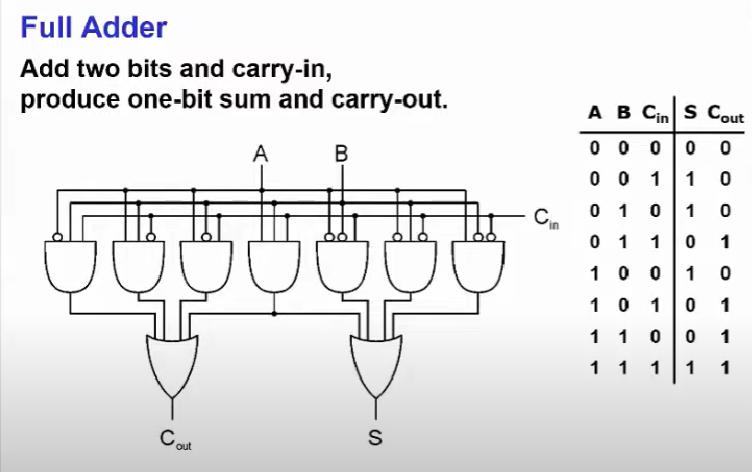
위 Full Adder를 바로 살펴보기 전에 Full Adder가 어떻게 구성되는지를 살펴보면
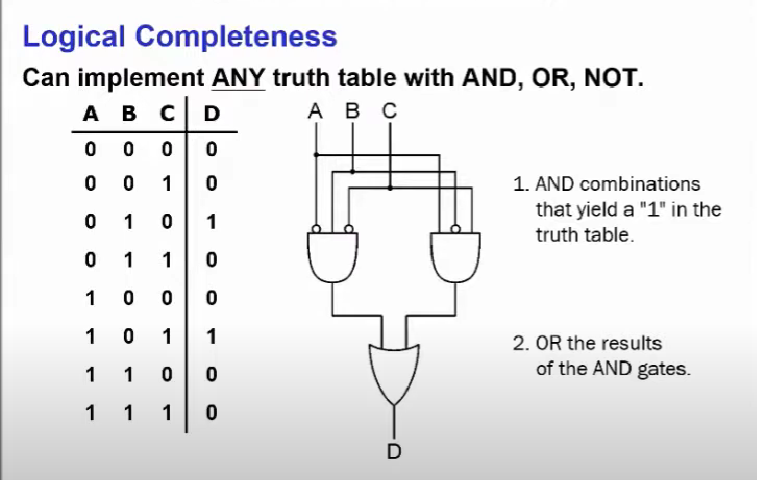
- AND combinations that yiedl a “1” in the truth table
- 위 이미지에서 출력값(D)가 1이 되는 것을 살펴보면 A, B, C가 0, 1, 0과 1, 0, 1이 있다. 그럼 입력값의 AND 연산을 통해 출력값을 1로 만들려면 0, 1, 0의 경우에는 not 0, 1, not 0이 되어야 and 연산에서 출력이 1이 되므로 그림 속 왼쪽 게이트와 같은 형태가 만들어지고
- 1, 0, 1의 경우에도 마찬가지로 1, not 0, 1이어야 and 연산에서 출력값이 1이므로 그림 속 오른쪽과 같은 게이트가 만들어지고
- OR the results of the AND gates 그 and 연산을 나온 출력값을 OR 연산을 하게 되면 출력이 1이 된다.
즉, 진리표 속에서 출력값이 1이 나오는 인풋 조합이 AND 연산을 통해 1이 나오려면 딱 그 조합만이 1이 나오고 나머지는 0이 나오게 되도록 만들어주는 것이다.

따라서 위 논리에 의해 Full Adder가 위 이미지처럼 이루어지는 이유를 살펴보자.
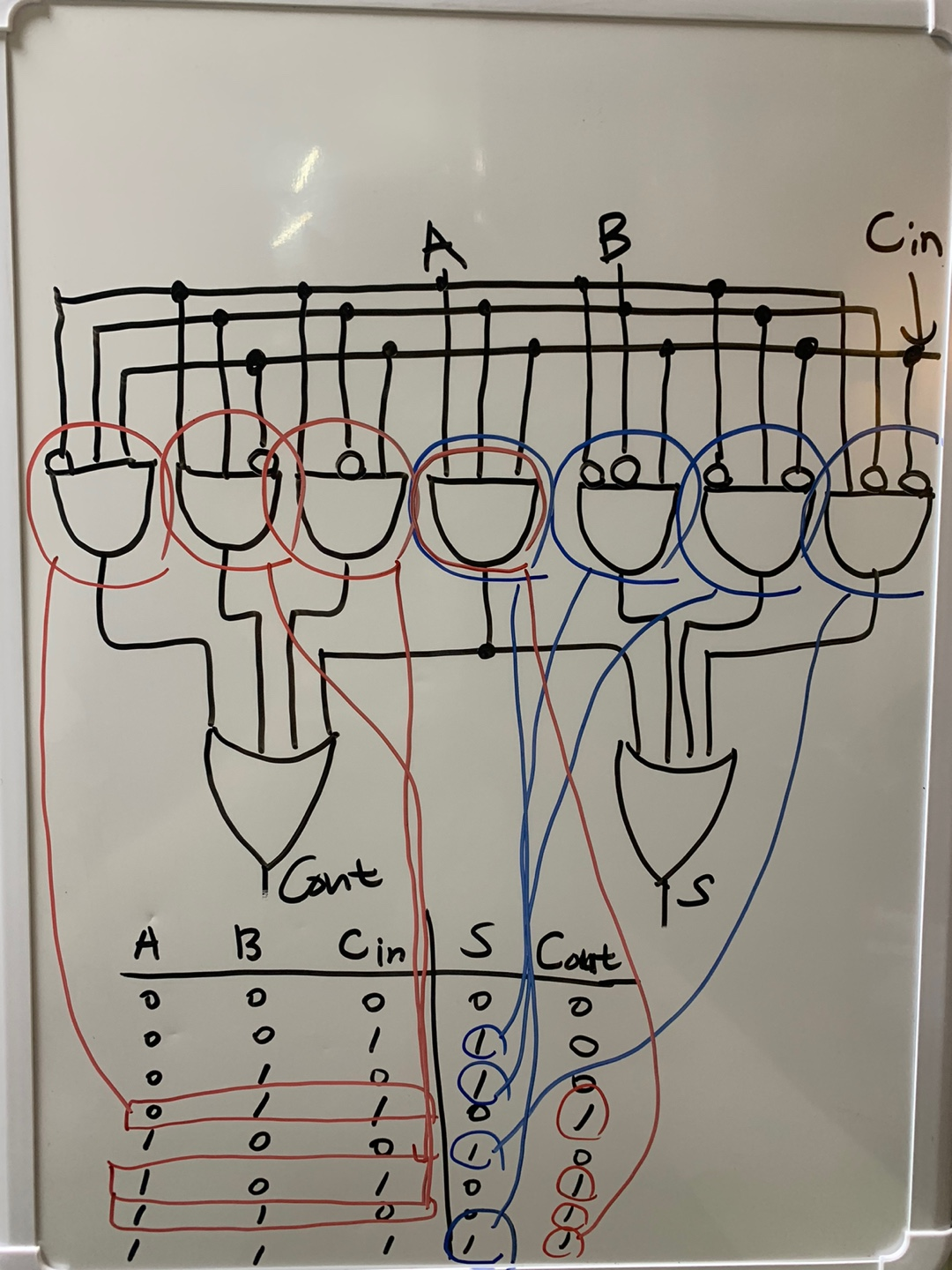
출력값이 S와 Carry out 으로 나눠지고 각 출력값이 1이 되는 인풋 조합을 찾고 해당 조합으로 and 연산이 1이 나오도록 하려면 어떻게 inverter를 적용시켜야할지 알 수 있으므로 위와 같이 Full Adder가 구성된다.

조합 논리 회로는 input 값이 주어지면 항상 동일한 출력값이 나오는 반면에 순차 논리 회로는 내부에 상태(정보)를 가지고 있어서 입력 값과 저장된 값에 따라 결과 값이 달라질 수 있다는 게 요지다.
예시로 들어 은행에 번호표를 뽑는 기계를 생각해볼 수 있는데, 번호표를 뽑을 때마다 숫자가 하나씩 올라가는 것이 예다. 즉, 이전 번호(상태)를 기반으로 출력값이 달라지는 것이다.
이 순차 논리 회로는 memory의 구성요소나 state machine의 구성요소로 유용하게 사용된다고 한다.
Sequential Logic Circuits
R-S Latch
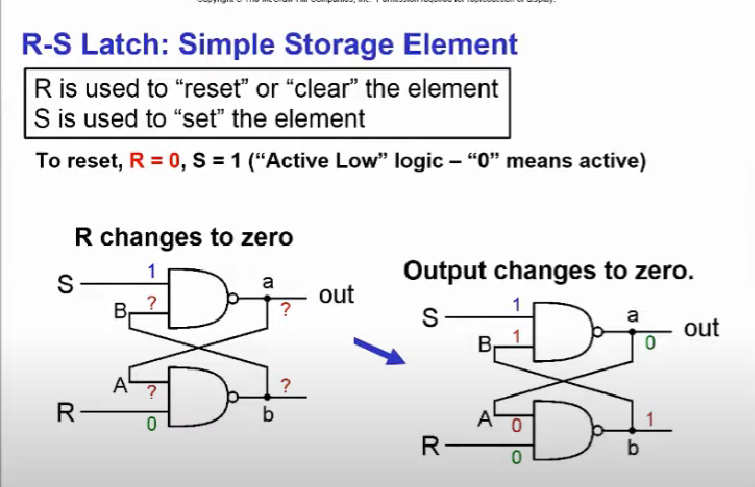
먼저 R(eset)-S(et) 래치를 살펴보자. 출력값을 리셋하려면 (0으로 만드려면) R에 0을 S에 1을 대입하면 출력값이 0으로 초기화 되는데 R이 0인 상태를 Active low logic이라고 칭한다.
즉, R에 0이면 AND 연산에 의해 출력이 0이 되고 NOT 연산에 의해 b가 1이 된다. 이 b가 S(1)과 and 연산을 통해 1이 출력되고 이를 not 연산에 의해 output이 0이 된다.
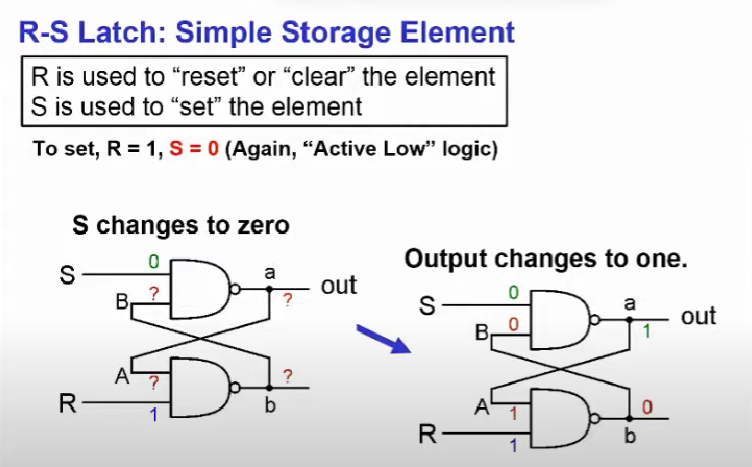
그리고 출력값을 1로 초기화 하려면 반대로 생각(R=1, S=0)하면 된다. S가 0이므로 위와 같이 AND 연산에 의해 B가 무엇이든 0이 출력되고 이를 NOT 하므로 출력이 1이 되며 a가 1이 므로 A가 1이 되고 R과 AND연산에 의해 1이 되지만 NOT 연산에 의해 b가 0이된다.
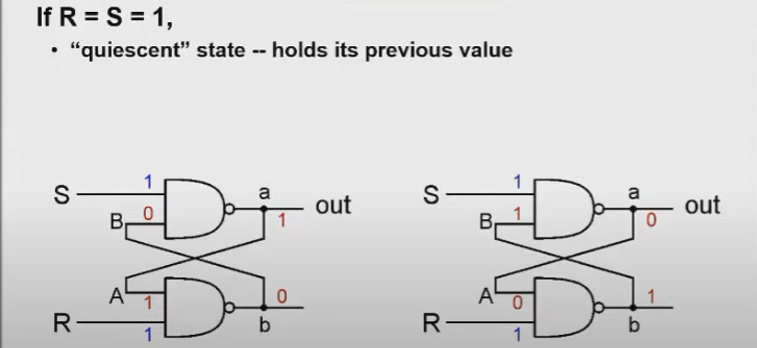
그리고 R과 S가 1일 때는 quiescent state라고 하여 이전 값을 그대로 보존한다.
회로를 보면 B가 0이고 A가 1일 때는 출력값이 a와 b가 1, 0으로 보존되고 반대도 마찬가지다.

이 때 하나 다루지 않은 조합이 있는데 R과 S가 둘 다 0일 때 인데
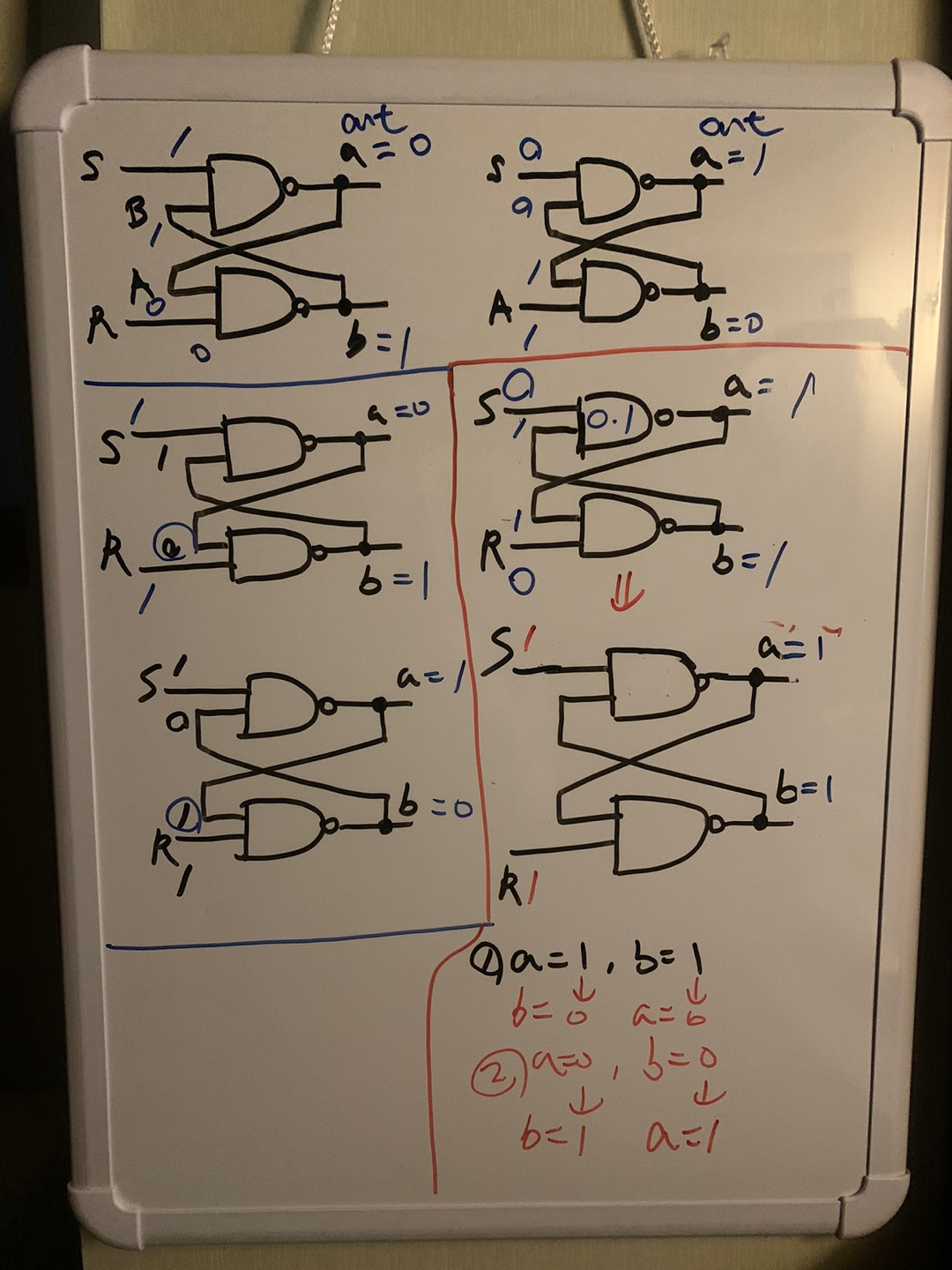
빨간색 박스를 보면 S랑 R이 0이면 a랑 b가 1이 된다. 문제가 되는 것은 이 때 R과 S를 1로 바꾸게 되면 a랑 b가 0이 되게 되고 이는 다시 a랑 b가 1이 되게 하면서 final state를 0과 1을 왔다 갔다하면서 결정하지 못하게 된다.
Gated D-Latch
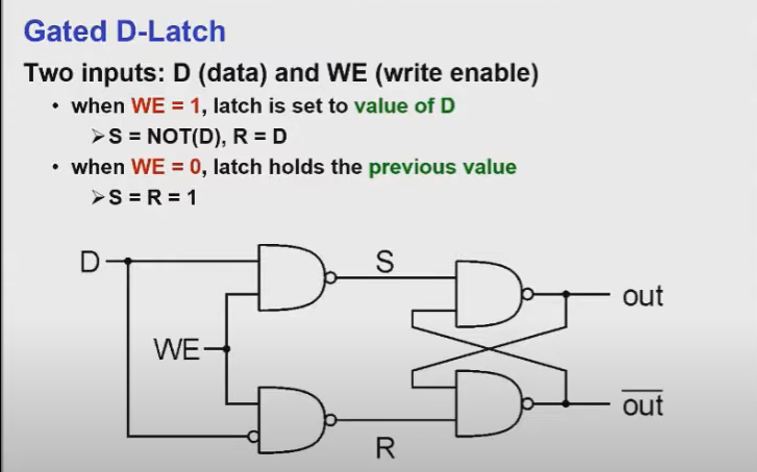
위에서 살펴봤던 R-S Latch를 컴포넌트로 하여 게이트를 추가해서 회로를 구성하게 되면 D-Latch를 만들 수 있다.
이 때 Input이 D(data)와 WE(write enable)가 추가되는데,
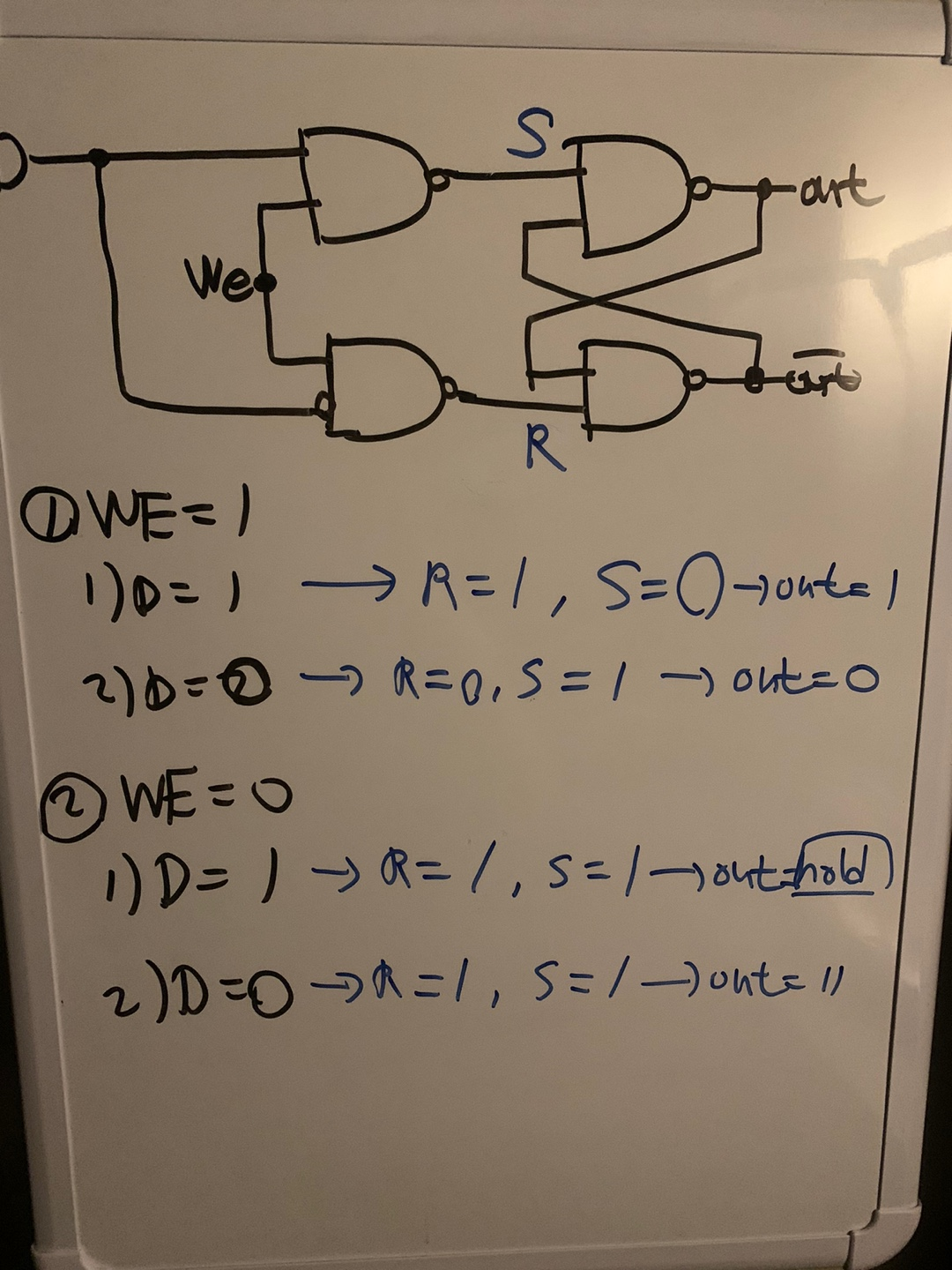
이미지 속 케이스에 따라 분기를 나눠 회로를 타서 R과 S값을 계산해보면 WE가 1일 때는 Latch의 출력값이 D가 되고 0일 때는 이전 값을 보존함을 알 수 있다.
Register
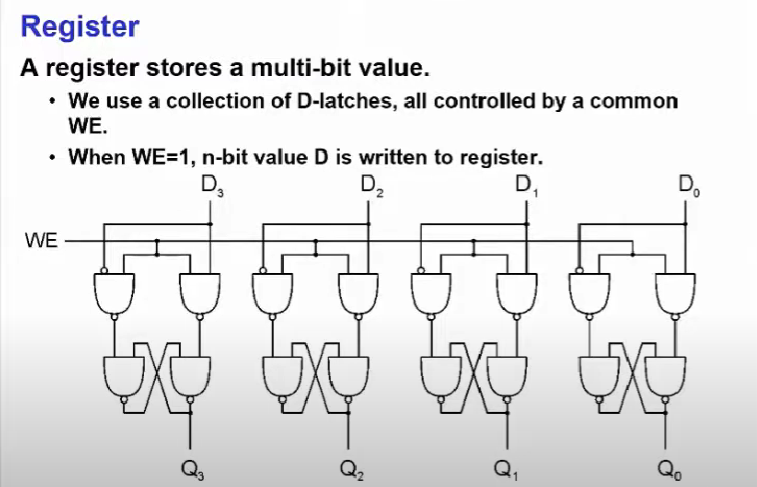
이제 이 Gate-D Latch를 이용해 Register를 만들 수 있다.
즉, D-Latch 와의 차이점은 입력값을 하나(1bit)만 다뤘지만 4개를 조합해 n-bit의 Data로 그에 맞는 출력값을 내보낼 수 있는 것이다.
D-Latch의 특성과 같이 Write Enable이 1이면 D(data)가 출력값이 된다.

그리고 이렇게 1bit가 아니라 n비트를 다루게 됨으로써 이를 표현할 필요성이 생기는데 위 이미지와 같이 N비트는 제일 오른쪽(0)부터 제일 왼쪽(N-1)까지 각 자릿 수를 표현할 수 있게 된다.
Memory
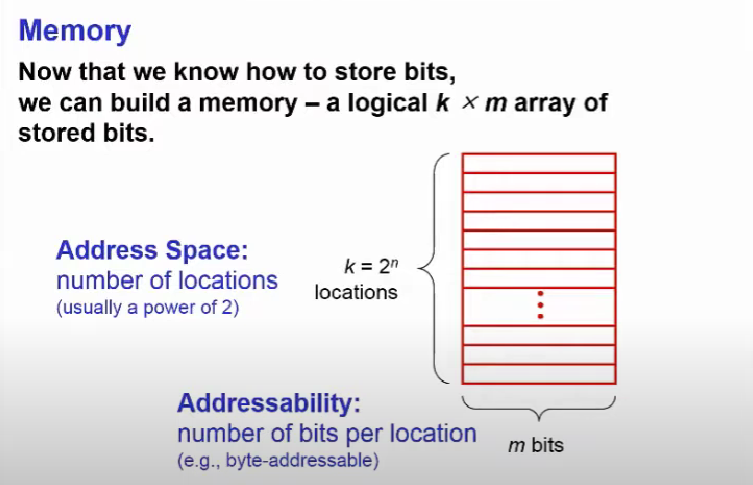
이제 bit를 어떻게 저장하는지 알게 됐으므로 memory를 만들 수 있다.
- location: address로 bit를 저장하는 공간을 의미.
- Addrees Space: 이러한 location의 수(2^n개).
- Addressability: 각 location 당 저장되는 bit의 수(m)를 의미.
이렇게 Memory는 k(2^n) X m으로 표현
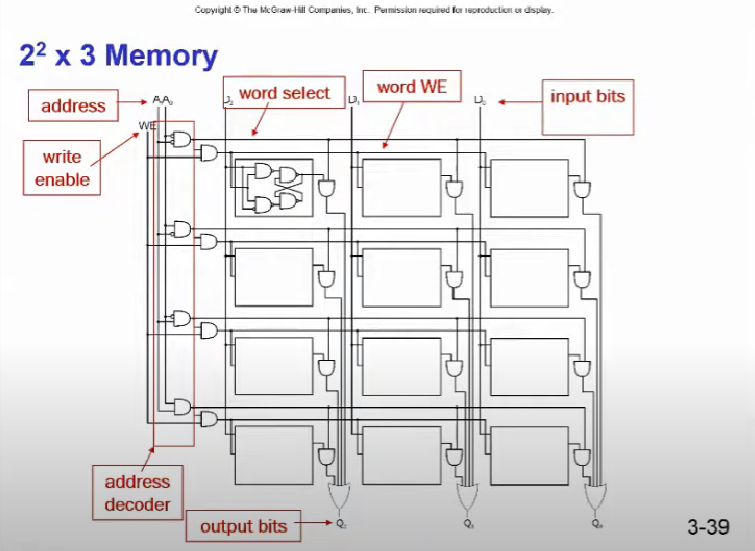
그 예시로 2^n x 3 Memory를 볼 수 있는데 Address Space 즉, location의 수가 4개이고 각 로켕션에 저장되는 비트가 3개로 구성되어 있는 메모리다.
More Memory Details

실제로는 위 그림처럼 D-Latch를 사용해 구현되진 않지만 이러한 논리적 구조는 매우 비슷하다고 한다.
RAM의 2가지 기본 종류로는 Static과 Dynamic있는데
일반 컴퓨터에서 사용하는 RAM은 Dynamic Ram이라고 한다. 느리지만 dense하다고 하며 가만히 냅두면 전자가 빠져나가 데이터를 잃을 수 있기 때문에 계속 refresh를 해줘야 한다고 한다.
그리고 전원을 끄게 되면 데이터가 날라가는 휘발성 메모리가 있고 비휘발성 메모리가 있는데 이 ram들은 비휘발성이다.
State Machine
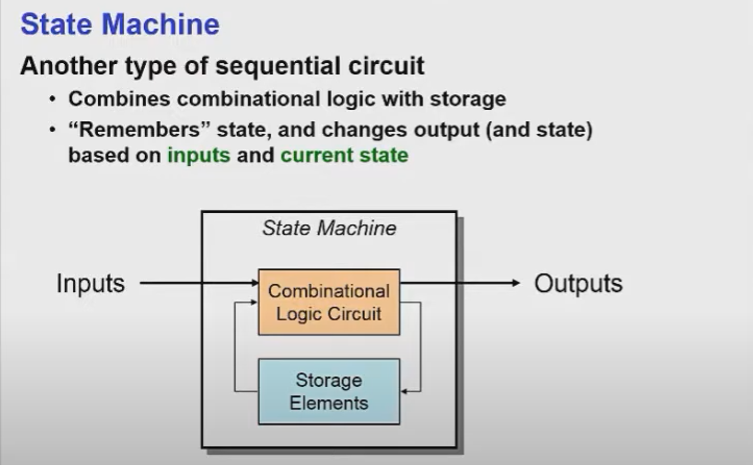
순차 회로의 또 다른 종류로는 State Machine이 있는데 Storage와 조합 로직 회로를 결합한 형태다.
이는 인풋과 현재 저장된 상태를 조합해 출력값이 바뀔 수 있다.
Combinational vs Sequential
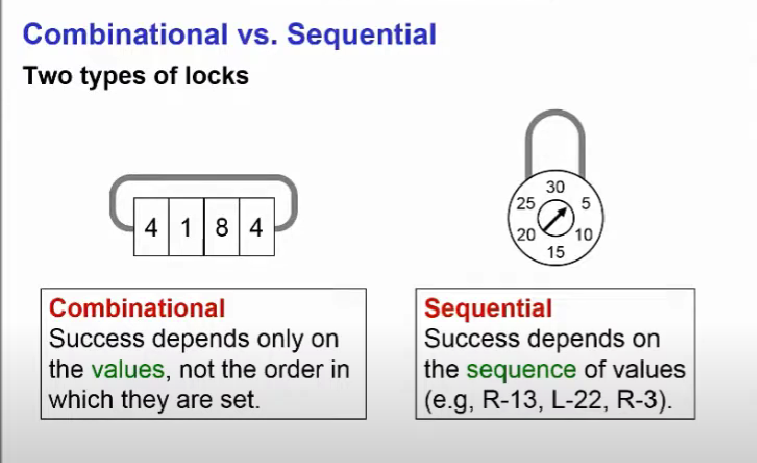
State 머신을 설명하기 위해 위 비유를 생각해볼 수 있는데, Combinatioanl은 자물쇠를 풀기 위해 4184 처럼 딱 이 조합으로만 자물쇠를 풀 수 있다. 하지만 Sequential의 경우에는 R-13, L-22, R-3처럼 값의 순서를 따라서 맞춰야 자물쇠가 열린다.

State를 개념적으로 설명하면 관련된 모든 요소의 snapshot이다. 예시로는 바둑을 둘 때 바둑판의 검, 흰돌의 배치, 누구 차롄지 등을 state라고 생각할 수 있다.

유한한 상태를 가지는 기계는 다음과 같은 구성요소로 설명될 수 있다.
- 유한한 수의 상태를 가져야 하고
- 유한한 외부 인풋이 있어야 하고
- 유한한 수의 외부 출력이 있어야 하고
- 모든 상태가 어떻게 변하는 지에 대한 설명
- 각 출력값이 결정되는 설명
Clock
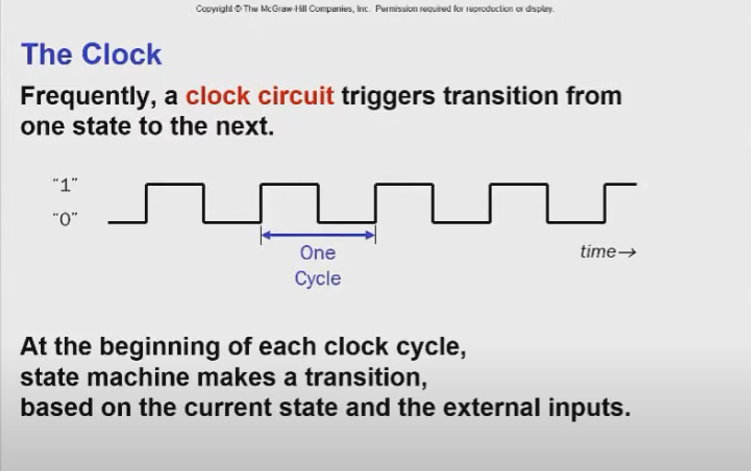
클락은 시간에 따라 0과 1을 출력하는 cycle을 반복하는 회로인데 사이클이 돌 때마다 state machie은 외부 인풋과 현재 상태에 기반해 상태를 transition하게 된다.
Storage Master-Slave Flipflop
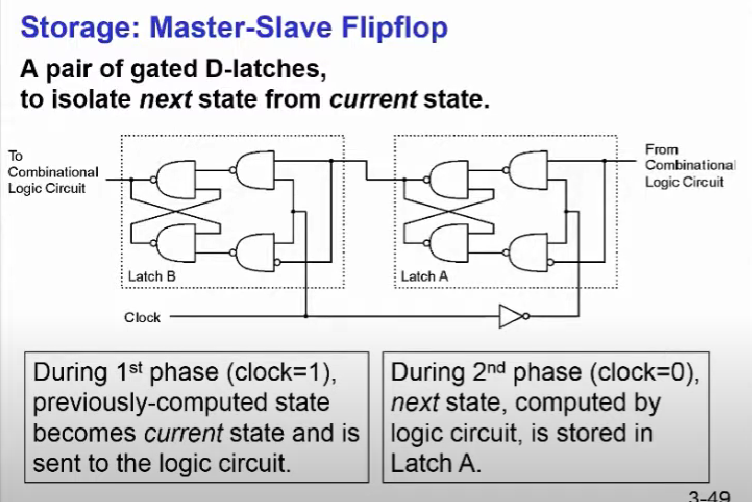
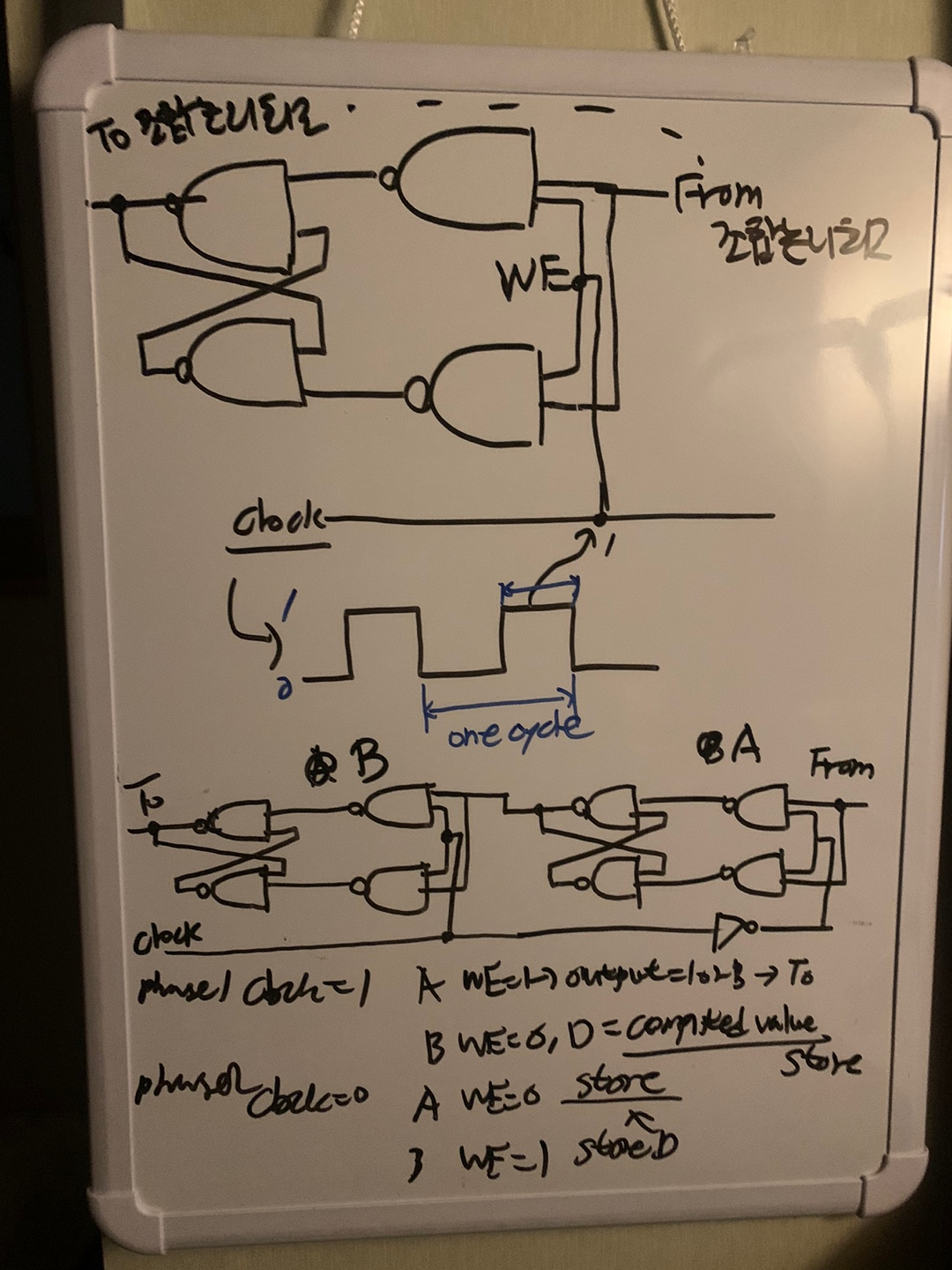
이게 필요한 이유는 Latch B가 하나만 있다고 상상해보자. 그럼 위 이미지에서 처럼 클락이 1이라고 가정했을 때 출력값을 조합 논리 회로로 보내게 되고 클락이 1인 구간이 끝나기 전에 다시 조합 논리 회로에서 계산된 값을 인풋으로 받아 아직 WE가 1이기 때문에(CLOCK이 1) 다시 계산된 값을 바탕으로 또 조합 논리 회로로 출력 값을 보내 상태가 계속 갱신되는 LOOP를 문제가 발생한다.
이를 해결하기 위해 위 이미지의 아래 그림처럼 Latch를 2개를 붙이고 Clock이 한 페이즈(1)일 때 not 연산을 통해 오른쪽 latch에 전달한다. 이렇게 되면
- phase가 1일 때는 Latch B에서 이전에 조합 논리 회로에서 계산된 값을 Latch A에서 전달받아 조합 논리 회로로 출력값을 보내게 된다.
- phase가 0일 때는 Latch B는 WE가 0이 되기 때문에 값을 HOLD하고 Latch A에서는 조합 논리 회로에서 받은 값을 저장해 놓는다.
이로써 루프가 도는 걸 방지할 수 있다.
예제!
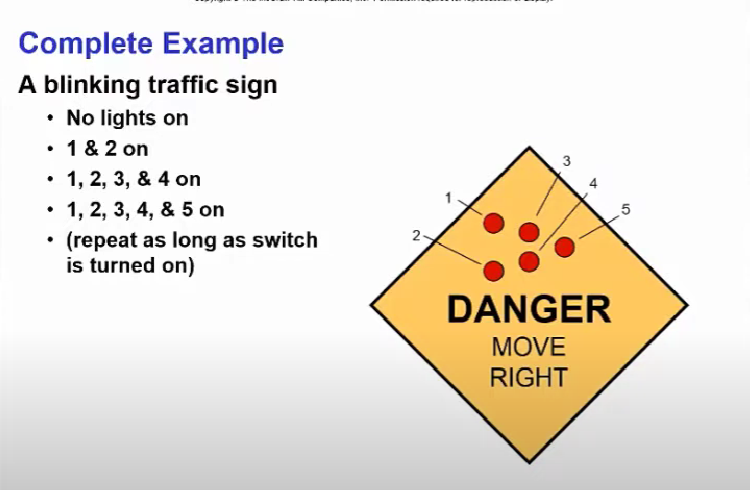
위 표지판을 보게 되면
- 불이 꺼져있고
- 1, 2가 켜지고
- 1, 2가 켜진 상태에서 3, 4가 켜지고
- 1, 2, 3, 4가 켜진 상태에서 5가 켜지고
- 1번 상태가 되고를 계속 반복하는 것이다.
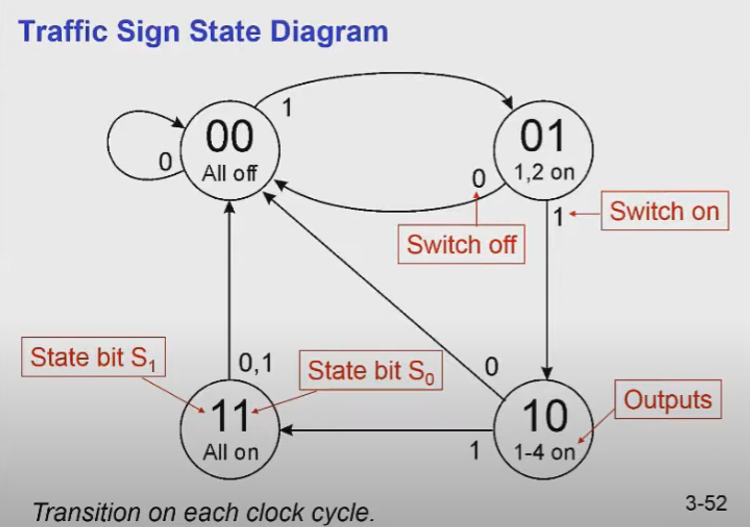
이를 상태 다이어그램으로 나타내보면
State bit가 2개이고
- 00일 때는 불이 꺼진 상태가 되고 switch가 open(0)이면 계속 00 상태가 반복되고 closed(1)이면 다음 상태인 01로 넘어간다.
- 그럼 불 1, 2가 켜지고 여기서 상태가 0이냐 1이냐에 따라 또 달라지는데 0이면 다시 00상태로 돌아가고 1이면 10상태인 1,2 가 켜져있는 상태에서 3, 4도 켜진다.
- 여기서도 switch가 0이면 다시 00으로 돌아가고 1이면 11 상태로 가지고
- 11에서는 스위치가 0이건 1이건 00으로 돌아가게 된다.
근데 사실 01, 이나 10은 살짝 억울한게 전 상태로 돌아가야 되는데 00으로 가는게 에러다.
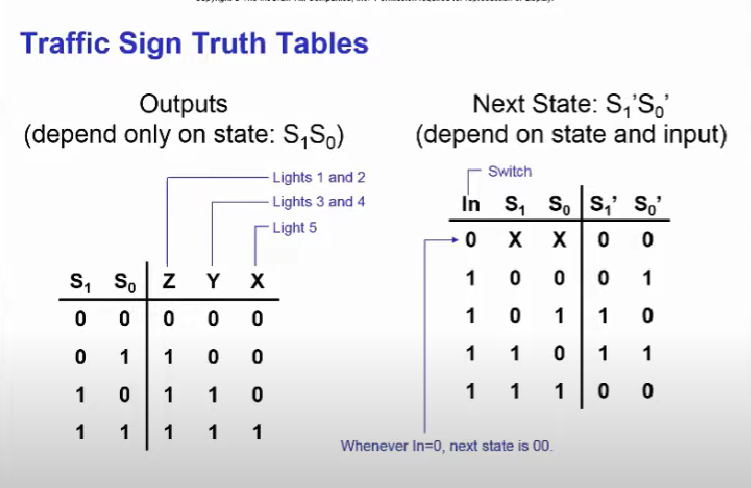
이걸 진리표로 나타내보면 State bit가 2개로 S1, S0이고 그에 따라 Output인 z, y, x로 나타내져 있다. 해석해보면 위 내용과 맞음을 알 수 있다.
그리고 Next State같은 경우에는 In은 Switch를 말하는데 0인 경우에는 S1과 S0이 XX로 되어 있는데 각 비트의 값이 무엇이든 그 값의 다음 상태가 00이라서 축약된 것이고
IN이 1인(스위치가 켜진 경우)에는 다이어그램에서 봤던 것 처럼 현재 State를 기준으로 다음 State를 예상해볼 수 있다.

댓글남기기