(비전공자 CS 공부) 컴퓨터과학과 실습 1편

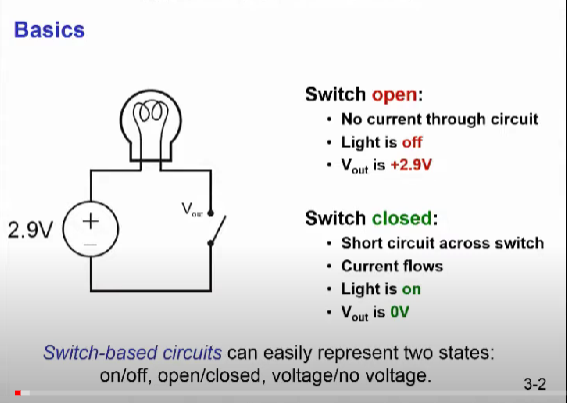
스위치에 기반한 회로는 binary(2가지) 상태를 쉽게 표현할 수 있는데, 스위치가 열려있으면 전류가 회로를 흐르지 않고 스위치가 닫혀있으면 전류가 회로를 흐른다.

위 내용에서 Vout이 2.9V라는 말은 스위치가 열려있어서 전류가 흐르지 않기 때문에 전구에서 전류를 사용하지 않아 전압 2.9V를 그래도 흘려보낸다는 뜻이다.

그럼 반대로 Switch가 closed 상태라면 전류가 흐르기 때문에 전구에서 전류를 사용함으로써 Vout이 0V가 된다.

이 내용은 아날로그의 전압을 디지털 Symbol로 할당하기 위한 내용이다. 즉 디지털은 0 또는 1의 값만 허용하기 때문에 아날로그 전압이 디지털에서 0또는 1이 되도록 판정 기준을 정함으로써 0과 1사이의 값을 허용하지 않도록 할 수 있다.

디지털 symbol 즉, 0과 1을 사용하는 컴퓨터 하드웨어 객체들은 전부 반도체로 이루어진다.

• 도체(conductor): 전류가 흐르는 물질
• 부도체(insulator): 전류가 흐르지 않는 물질
• 반도체(semiconductor): 전류가 흐를 수도 흐르지 않을 수도 있는 중간 정도 성질의 물질.

이 때 반도체는 실리콘이라는 원소로 이루어져 있는데 실온에서는 전류가 발생하지 않는다. 그래서 전기가 흐르게 하기 위해서는 150도 이상의 열을 가해야 하는데, 컴퓨터 내부에서 150도의 열을 매번 가해줄 순 없으니 이를 해결하기 위한 방법이 다음에 나온다.

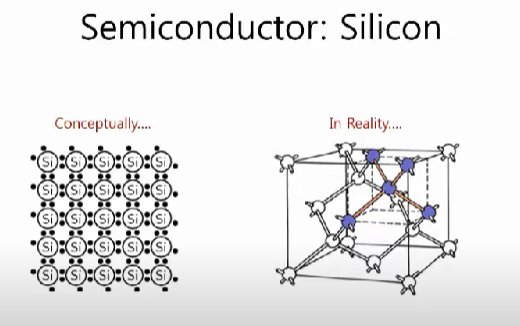
실리콘의 최외각 전자는 4개로 위 이미지와 같이 실리콘 주변으로 4개의 실리콘이 모이게 되면 최외각 전자가 8개를 이루며 안정된 상태가 된다. 하지만 이 상태에선 전자가 움직일 수 없는데,

위 이미지와 같이 최외각 전자가 5개인 원소를 넣어주게 되면 전자가 하나 남기 때문에 자유롭게 이동할 수 있게 되는데 이를 n-type 반도체라고 한다.

전류가 흐르는 원리는 실온에서 자유 전자가 한쪽 방향에서 다른 방향으로 흐를 수 있고 이를 반복할 수 있기 때문임.

그리고 최외각 전자가 3개인 붕소를 넣어주게 되면 최외각 전자가 7개가 되면서 1개의 양공이 발생하게 되는데(위 이미지에서는 hole)이라고 칭함. 이를 p-type 반도체라고 하고 전압을 가하게 되면 다른 자리에 있던 전자가 양공을 채우기 위해 움직여 전자가 흐르게 된다.

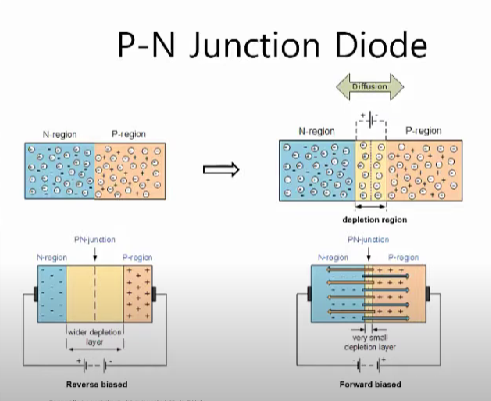
n타입 반도체와 p타입 반도체를 접합(Junction)하게 되면, 위 이미지와 같이 Diffusion 영역이 생기게 되는데 잠시 아래 배경지식을 깔고 설명을 이어가보자.

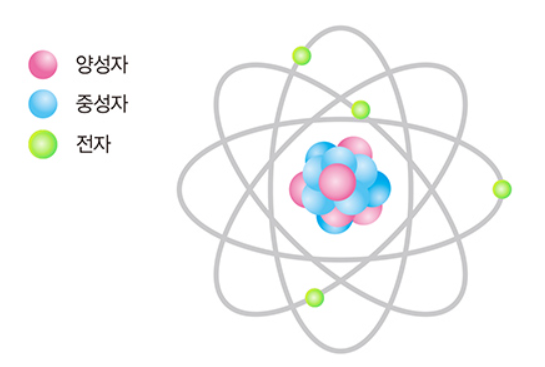
만물을 구성하는 기본 입자는 ‘원자’로 원자핵과 그 주위를 맴도는 전자로 구성된다.

• 원자핵은 양성자와 중성자로 구성되며 양성자는 양(+)의 성질을 띠고 있고 전자와 같은 개수로 존재하기 때문에 원자는 전기적으로 중성이다.
• 전자는 음(-)의 성질을 띠며 매우 가벼운 것이 특징이다.

다시 위 이미지에서 N형과 P형 반도체를 접합하게 되면 전자는 높은 농도(N형은 전자가 많은 상태라 음전하를 띠고 P형은 전자가 하나 부족한 상태인 양공이 많아 상대적으로 양전하를 띰)에서 낮은 농도로 이동하려는 성질이 있어 N형 반도체의 전자가 P형의 양공쪽으로 P형 반도체의 양공이 N형 반도체 쪽으로 흐르는 현상이 일어나고 이 때 이동하다가 전자와 양공이 만나 결합하여 접합 부근에는 중성을 띠는 depletion region이 만들어진다.

이 상태에서 N형 반도체는 음전하를 띄기 때문에 음 전압을 P형에는 양전압을 가하게 되면 서로를 밀어내는 힘으로 인해 depletion region이 줄어들게 되면서 전자의 이동이 일어나며 전류가 발생하게 되는 것이다.

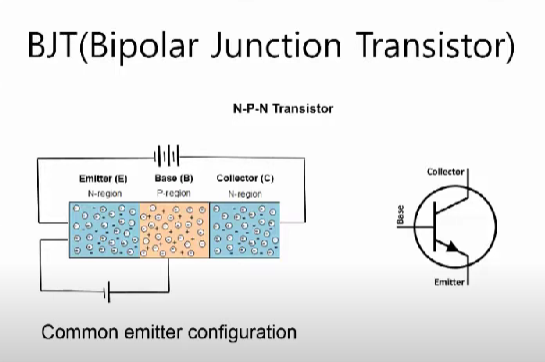
그리고 위 이미지와 같이 전압을 걸어주게 되면 트랜지스터의 아래 부근에는 약한 전류가 발생하는데 윗 부분에는 큰 전류가 발생하게 되어 작은 전압으로도 큰 전류를 발생시킬 수 있는 NPN 트랜지스터라는 게 있다고 한다.

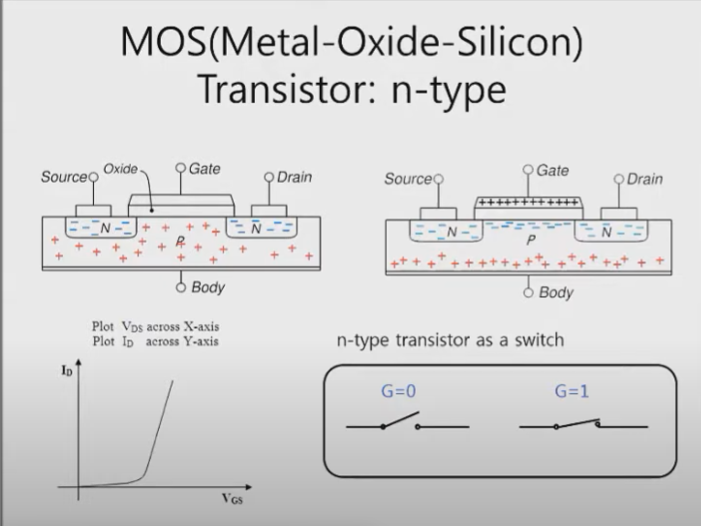
새로운 조합인 MOS(Metal-Oxide-Silicon) 트랜지스터를 볼 수 있는데, Source와 Drain은 전류가 들어왔다가 나갈 수 있는 출구고 Gate는 도체인 금속이며 Oxide는 유리와 같은 부도체로 우리 머리카락 보다 얇게 깔려있다고 한다.

이 때 아래에는 p형 반도체와 n형 반도체 두 영역을 볼 수 있는데 앞에서 살펴본 바와 같이 depletion region이 일어나기 때문에 가만히 냅두면 전류는 발생하지 않는다.

이 때 금속인 Gate에 + 전압을 걸어주게 되면 P형 반도체를 이루고 있는 원소들의 일부 전자들이 gate쪽으로 모이게 되고 이는 N형 반도체는 자유 전자가 많은 물질이었으므로 도체와 같아 Source와 Drain사이에 전류가 흐를 수 있게 되는데 이를 channel이라고 한다.

따라서 이를 Gate에 전압을 가했을 때는 전류가 흐르기 때문에 스위치를 closed한 것과 같이 1로 표현할 수 있고 전압을 가하지 않았을 때(0)는 스위치가 open 된 것과 같이 여길 수 있다.

BJT 경우에는 수식이나 사용법이 복잡해 라디오와 같은 곳에 쓰이고 있지만 MOS 트랜지스터는 CPU에 몇천억개가 사용되고 있다고 한다.

즉, 완벽함은 더할 게 없는 게 아니라 더 이상 뺄 것이 없을 때 달성된다는 교훈을 말해주고 싶었다고 한다!

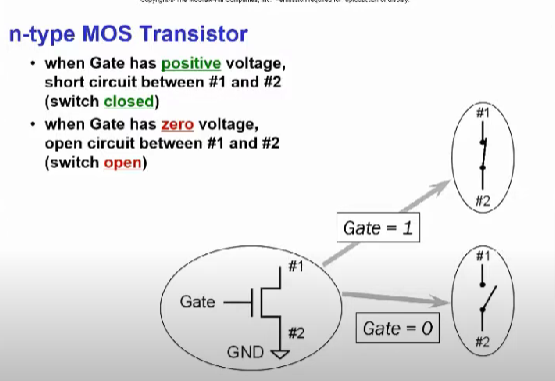
MOS Transistor에서 볼 수 있었듯이 전류는 n type 반도체 사이에서 흐르기 때문에 n type MOS 트랜지스터라고 명한다.

이를 다이어그램으로 표현하면 위 그림과 같은데 게이트에 + 전압을 걸어주면 N형 반도체 사이에 전류가 발생하기 때문에 스위치가 closed 된 것과 같으므로 Gate = 1로 표현할 수 있고

반대로 gate에 전압을 걸지 않으면 전자가 흐르지 않기 때문에 스위치가 open된 것과 같기 때문에 Gate=0으로 표현할 수 있다.

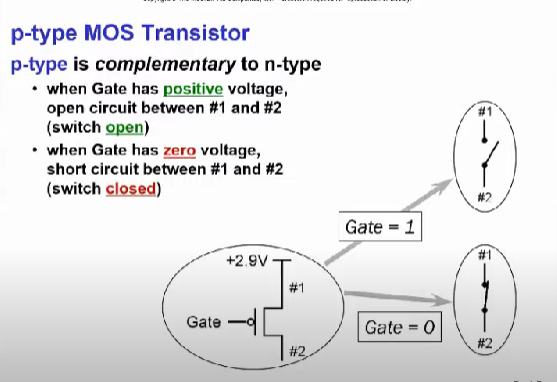
p-type MOS 트랜지스터는 반대로 생각해볼 수 있다. Gate에 + 전압을 가하면 스위치가 open되고 전압을 가하지 않으면 스위치가 closed 되는 것이다.

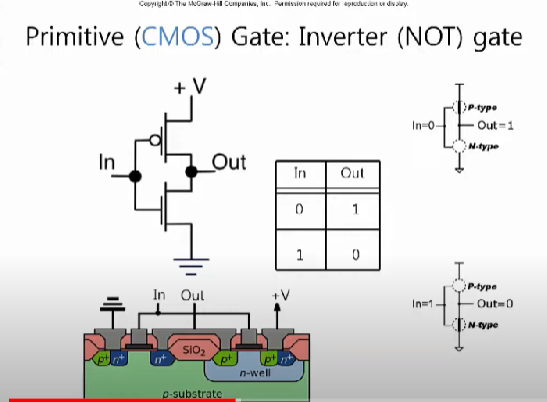
이렇게 p타입과 n타입 트랜지스터를 가지고 더 복잡한 회로를 만들 수 있는데 Inverter 즉, Not Gate를 만들 수 있다.

p타입과 n타입 트랜지스터를 위 이미지와 같이 연결하게 되면

• Input으로 0이 주어질 경우:
  • p-type은 gate가 0일 경우에 switch가 closed 즉, 전류가 흐르게 되어 +V로 전류가 흐르기에 값이 1이 되고
  • n-type은 gate가 0일 경우에 전류가 흐르지 않기 때문에 출력이 0으로 생각할 수 있기에 switch가 open되어 끊어진 것으로 생각할 수 있다. 따라서 output은 1이 된다.
• Input으로 1이 주어질 경우:
  • p-type은 gate가 1일 경우에 switch가 open되는 것과 같이 끊어져 전류가 흐르지 않게 되고
    • n-type은 Source와 Drain 사이의 전류가 흐르게 되어 접지로 전류가 흘러 출력이 0이 된다.

위 이미지의 전류 흐름 예시

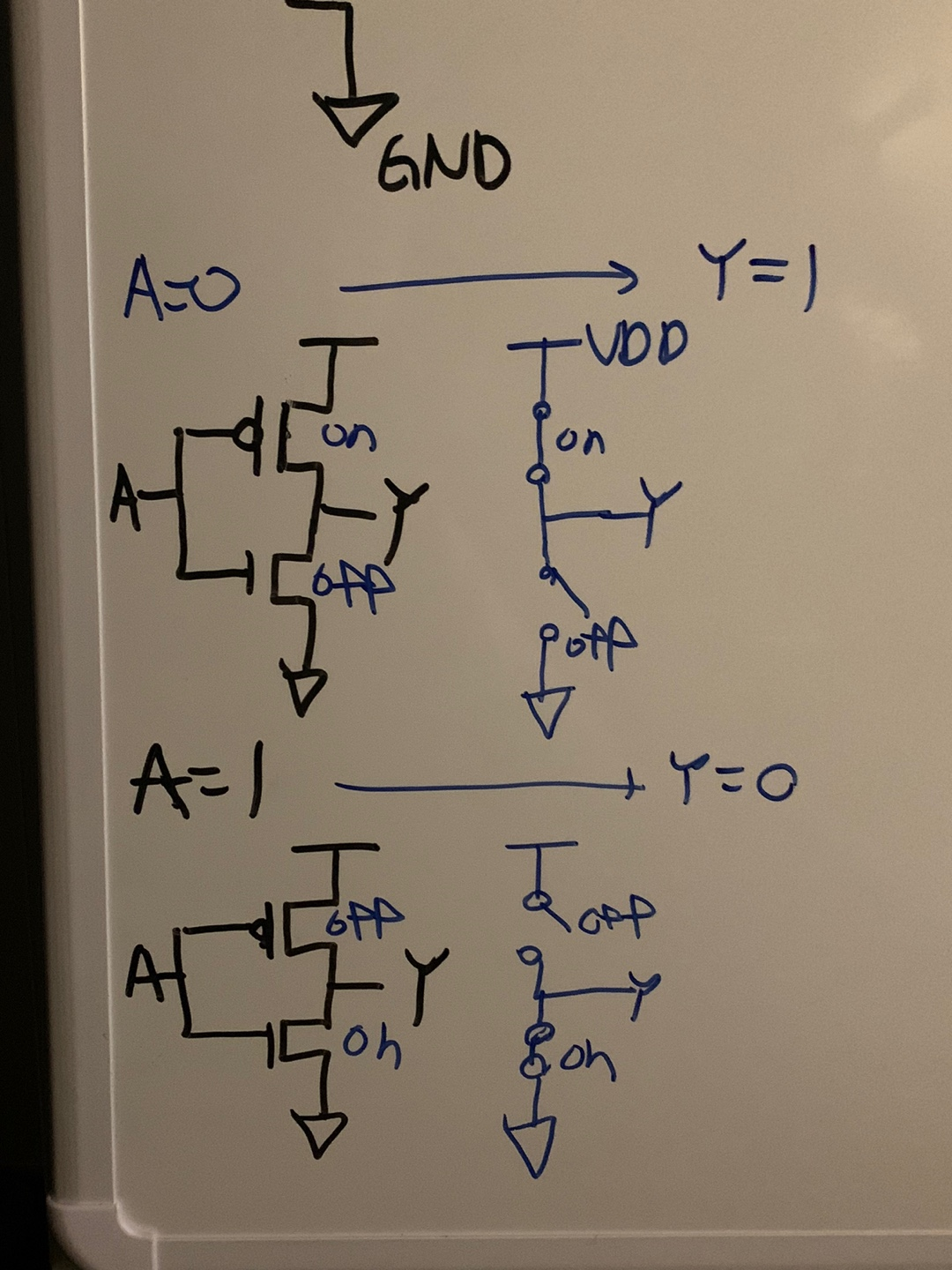
그렇게 만든 NOT GATE에 대한 회로는 일반화할 수 있는데 이를 CMOS 회로라고 칭한다.

이 때 원리는 위에서 봤듯이 input이 0이 되면 p형 mos의 전류가 흘러 VDD로 부터 전류를 받아 출력이 1이 되고 대신 NMOS는 전류가 흐르지 않는다. INPUT이 1이 되면 PMOS는 끊어지고 NMOS는 연결되어 접지(GND)로 전류가 흐르게 되어 출력이 0이 된다.

이 때 중요한 점은 인풋에 따라 PMOS 또는 NMOS가 확실히 전류가 흐르거나 흐르지 않게 되어야한다는 점이다.

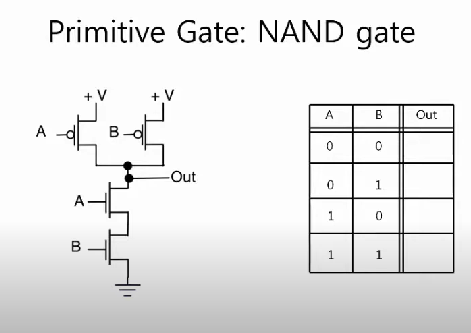
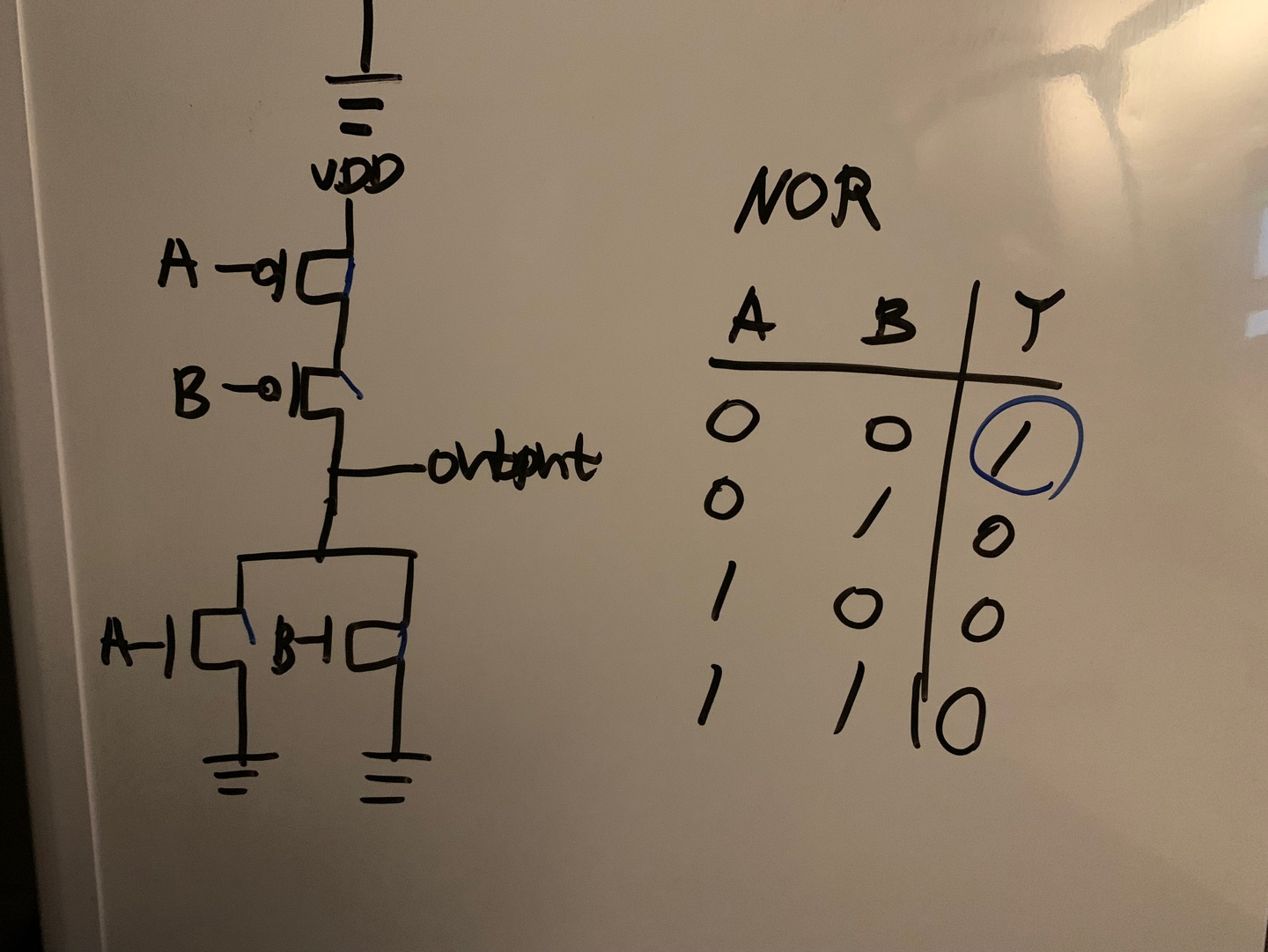
그리고 PMOS를 병렬로 NMOS를 직렬로 연결하면 NAND gate를 만들 수 있다. 오른쪽 진리표의 각 행의 A와 B 인풋을 대입해보면 되는데,

1) A, B 둘 다 0인 경우 A랑 B가 둘 다 0이면 NMOS에서는 Channel이 형성되지 않아 전류가 흐르지 않기 때문에 끊어지는 것으로 생각할 수 있고 PMOS는 반대기 때문에 A와 B 둘 다 스위치가 연결되어 +V가 OUTPUT으로 흘러 출력 값이 1이 된다. 2) A = 0, B = 1인 경우 A가 0이기 때문에 NMOS는 끊어진 것과 마찬가지고 PMOS는 연결되기 때문에 출력이 1이 된다. 3) 2)의 반대인 경우 2)의 반대로 생각하면 되기 때문에 PMOS가 병렬로 연결되어 있어 B에서 +V가 출력값으로 1이 된다. 4) 1)의 반대인 경우 PMOS가 다 끊어지고 NMOS가 연결되기 때문에 전류가 GND로 흘러 출력이 0이된다.

즉, 이는 논리 AND 연산의 결과값의 반대이므로 NAND 연산의 결과를 만들 수 있게 된다.

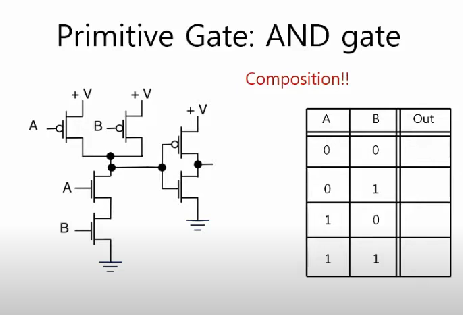
NAND를 얻었으니 NAND의 반대인 AND를 구하려면 우리가 앞서 구현했던 INVERTER를 합성해서 NAND 출력값의 반대값을 출력하도록 만들 수 있다.

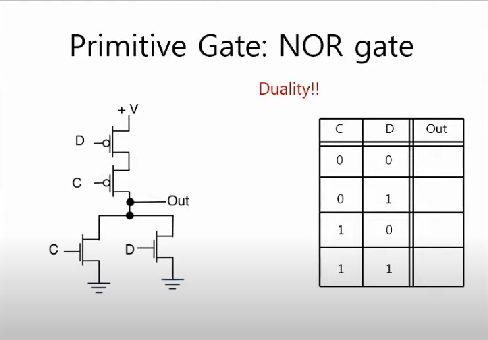
그리고 NOR gate는 위 이미지와 같이 pmos를 직렬로 nmos를 병렬로 연결하면 된다. 마찬가지로 NOR gate의 출력값에 인버터를 붙이게 되면 OR gate를 만들 수 있다.

흐름을 정리하자면 반도체에서 시작해 n, p타입 트랜지스터를 봤고 이를 결합한 NMOS와 PMOS를 만들었고 이를 조합해서 INVERTER, NAND, NOR 게이트를 만든 후에 INVERTER를 합성해 AND와 OR gate를 만들 수 있었다.

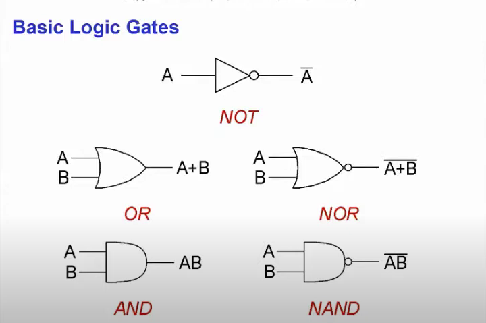
• NOT은 입력에서 출력으로 전류가 흐르는 삼각형 모양 뒤에 o를 붙여서 나타내고
• OR는 A+B(논리합), AND는 AB(논리곱)을 나타내고
• NOR와 NAND는 OR와 AND 위에 바(NOT을 의미)를 씌워준다

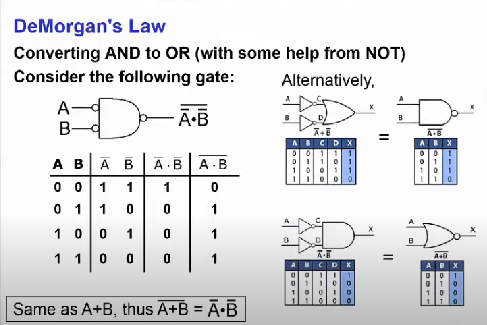
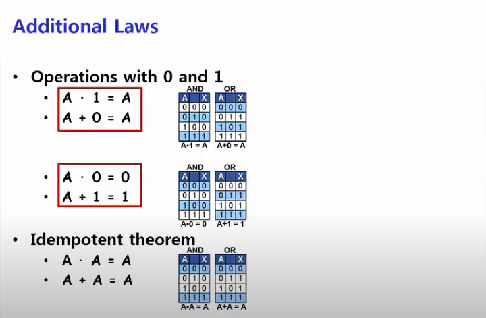
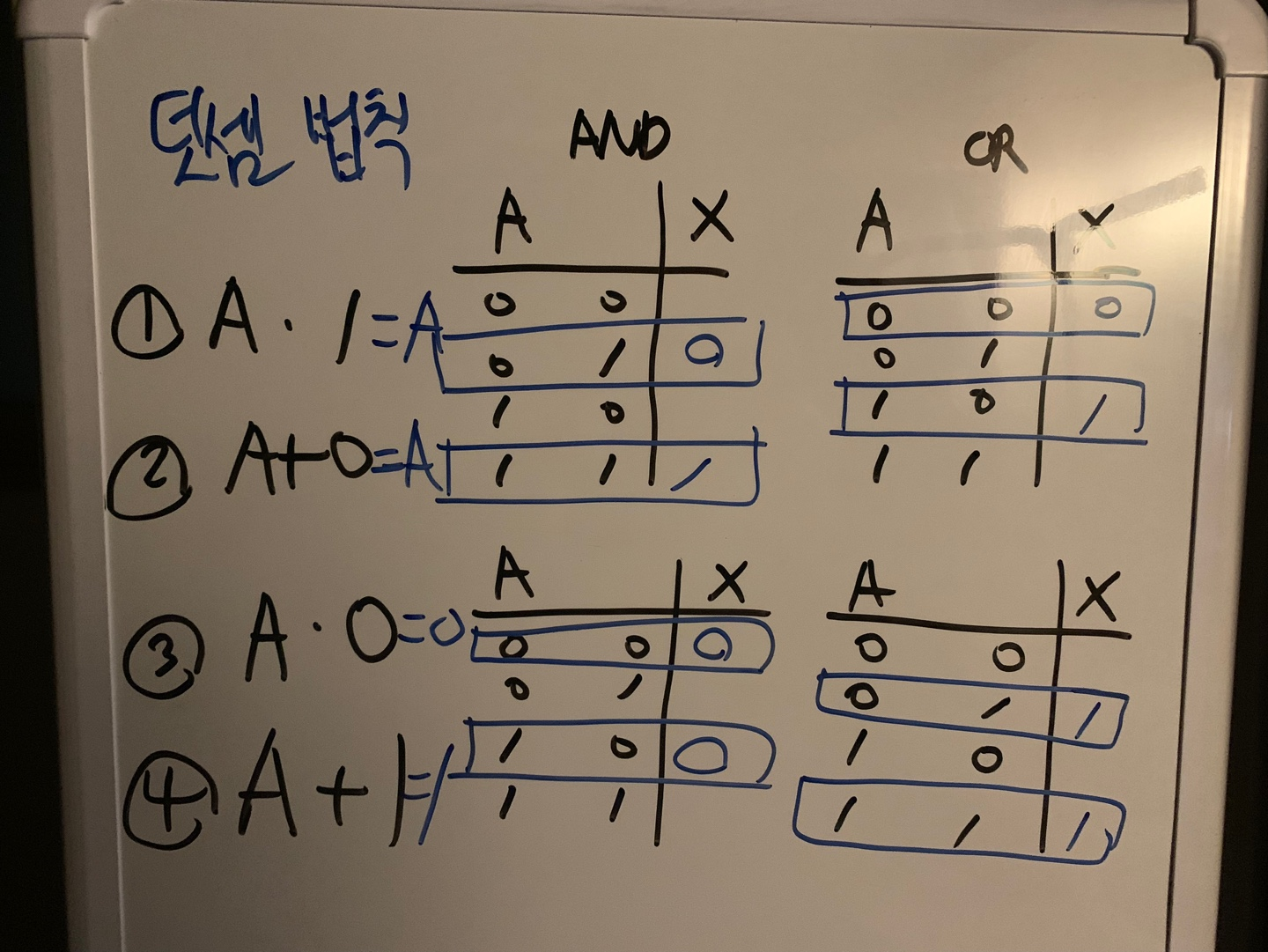
위 이미지는 위 PPT 자료에서 보이는 법칙을 진리표로 확인해본 것이다.

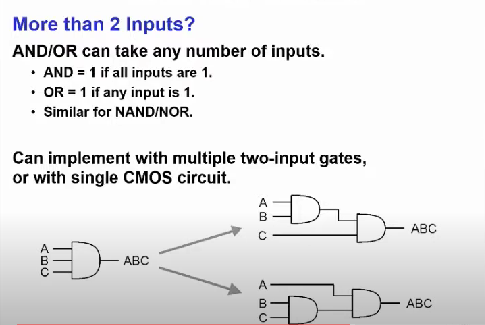
그리고 AND와 OR는 여려 개의 인풋을 가질 수 있다. 어차피 AND는 모든 인풋이 1이여야 출력이 1이고 OR는 인풋 중 1개만 1이어도 출력이 1이다.

이 때까지 2가지 인풋만 살펴봤는데 인풋이 3가지면 어떻게 할까? 이 때는 2개의 인풋 게이트 또는 하나의 CMOS 회로로 구현할 수 있다.

이렇게 우리가 배운 논리 GATE로 논리 회로를 구성할 수 있는데 논리 회로에는 위에서 볼 수 있듯이 2가지 종류가 있다.

• Combinational Logic Circuit
  • 전류의 입력값에 출력값이 의존하기 때문에 출력값이 정해져 있는 형태다. 즉, 회로 내 전류의 상태를 가지고 있지 않다.
• Sequential Logic Circuit
  • 출력은 인풋의 시퀀스(이전 또는 현재)에 따라 다를 수 있다.
  • 즉, 이전 input으로 부터 상태를 가지고 있을 수 있다.

그리고 유용한 combinational circuit를 살펴보고 sequential circuits를 살펴보기로 하는데 한 호흡 끊고 다음 편에서 보도록 합시다!